一、预备知识
了解红黑树之前,我们需要明白何为二叉查找树,何为平衡二叉查找树,何为左旋、右旋和双旋。
下面给出左旋、右旋和双旋转的简单示意图:
左旋:
当平衡二叉树中插入节点后,右子树的高度与左子树的高度之差大于2,则需进行左旋。
图示:
右旋:
当平衡二叉树中插入节点后,左子树的高度与右子树的高度之差大于2,则需进行右旋。
图示:
双旋转:
拿左旋情况来说,如果当前根结点的右子树的左子树的高度大于右子树,则在需要先对根结点的右子树进行右旋转,再整体左旋。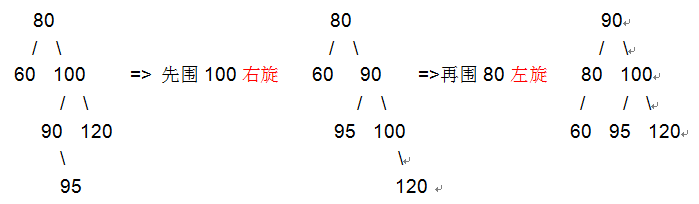
代码实现:
GitHub
二、红黑树
1.概念
红黑树同样是平衡二叉查找树,只是其实现平衡的算法不同,且不满足绝对平衡。其插入删除涉及到旋转的操作更少。
红黑树在结点中增加了一个存储位用来存储颜色,可以是RED或者BLACK,通过颜色及性质的约束,其可以保证它的最长路径不超过最短路径的二倍。
2.性质
- 每个节点颜色不是黑色就是红色
- 根结点是黑色的
- 如果一个结点是红色,那么它的子节点必定是黑色。(也就是没有连续的红结点)
- 每个叶子结点都是黑色
- 任意结点到每个叶子结点的路径都包含数量相同的黑节点。
3.插入操作
插入操作首先需要定位插入的位置,然后通过旋转、染色的操作实现自平衡。查找插入的位置并不难。
找到插入的位置后,我们需要明白插入的结点必定为红色(如果为黑色,黑色平衡被打破,很难处理)。
插入操作分为很多种情况,但整体上可分为三种:不需要处理、
不需要处理的情况:
- 红黑树为空树:直接把插入节点设为根结点,并且将其颜色染为黑色。
- 插入结点的父节点为黑结点:直接插入
- 插入结点已存在:把插入结点的颜色设为当前结点的颜色,更新当前结点的值为插入结点的值。
插入结点的父结点为红结点:
首先我们要明白如果父结点为红结点,那么该父结点肯定不是根结点,也就是说待插入结点肯定存在祖父结点,且祖父结点肯定为黑色。
根据待插入结点的叔叔结点的不同情况,可分为如下几种情况:
1)叔叔结点存在且为红色
这种情形的处理办法为:将祖父结点PP染红,父结点和叔叔染黑,使其变为红黑黑的结构。如下图所示:

进行此操作后,如果祖父结点的父结点为黑色,则不需再进行进一步操作。如果祖父结点的父结点为红色,则还需把祖父结点当做新插入的结点左自平衡处理,直到平衡为止。
也就是说红黑树的生长是自底向上的。
如果祖父结点刚好为根结点,则需要把祖父结点染黑。这是唯一会增加红黑树黑色结点层数的情况。
2)叔叔结点不存在或为黑结点,父结点是祖父结点的左子结点
- 插入结点是其父结点的左子结点:进行右旋
具体步骤为:将P染为黑色,PP染为红色,右旋。
- 插入结点是其父结点的右子结点:对P左旋使其转换为上一情形
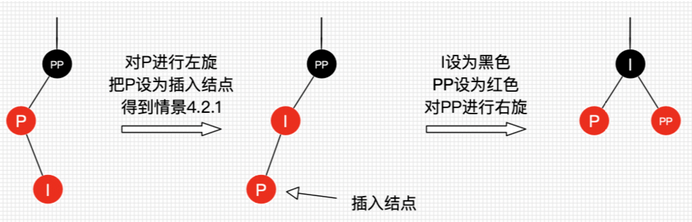
3)叔叔结点不存在或为黑结点,父结点是祖父结点的右子结点。
此情况与情况2)相反。
参考
https://blog.csdn.net/tanrui519521/article/details/80980135
https://blog.csdn.net/qq_37934101/article/details/81160254
https://www.jianshu.com/p/e136ec79235c